Introduction
This post is a comprehensive guide to conducting moderation analysis in SPSS. Moderation analysis is a vital technique for researchers seeking to understand the conditions under which relationships between variables exist. In this post, you will learn:
- The concept of moderation analysis, including its purpose and assumptions.
- How to use traditional regression models for moderation analysis.
- The advantages of using the Hayes PROCESS Macro.
- A step-by-step guide for conducting moderation analysis using SPSS.
- How to interpret results, including interaction terms and conditional effects.
Whether you are new to moderation analysis or looking to enhance your statistical skills, this guide provides practical insights and tools to make your analysis straightforward and effective.
1. How to Run Moderation Analysis in SPSS
Moderation analysis is a powerful tool for researchers aiming to uncover the conditions under which a specific relationship holds true. By incorporating a moderator variable, this analysis method enables an exploration of how external factors influence the dynamics between independent and dependent variables. Whether you are investigating social, psychological, or business phenomena, understanding moderation can provide critical insights into complex relationships. This guide will walk you through the theoretical foundations, practical steps, and tools required to conduct moderation analysis in SPSS. From traditional regression models to the widely used Hayes PROCESS Macro, you will gain the knowledge needed to perform and interpret this analysis effectively.
2. What is Moderation Analysis?
Moderation analysis is a statistical technique used to examine whether the relationship between two variables changes depending on the level of a third variable, known as the moderator. This method allows researchers to understand how external factors influence the strength or direction of a primary relationship.
Purpose of Moderation Analysis:
The main goal is to explore the conditions under which a specific effect occurs. For example, moderation analysis can reveal if the effect of stress on job performance varies depending on the level of support from colleagues.
Key Assumptions:
- The data must be continuous or categorical (properly coded).
- The relationship between the independent and dependent variables should be linear.
- No multicollinearity between the predictor and moderator variables.
- Homoscedasticity of residuals.
Traditional Regression Model
The traditional regression model is the starting point for conducting moderation analysis. In this method, the interaction term between the predictor and moderator is included in the regression equation:
Y = b0 + b1X + b2M + b3(X*M) + e
Where:
- Y = Dependent variable (Outcome)
- X = Independent variable (Predictor)
- M = Moderator variable
- X*M = Interaction term
- b1, b2, b3 = Regression coefficients
- e = Error term
By analysing the interaction term (b3), researchers can determine whether the moderator significantly influences the relationship between X and Y.
Hayes PROCESS Macro
The Hayes PROCESS Macro is an advanced statistical tool that simplifies moderation and mediation analyses in SPSS. Developed by Andrew F. Hayes, this macro provides a user-friendly interface to run moderation analysis without manually calculating interaction terms.
How to Set Up Hayes PROCESS Macro in SPSS:
- Download the Macro: Visit Andrew F. Hayes’ official website to download the PROCESS macro file (usually named “process.spd”).
- Install the Macro in SPSS:
- Open SPSS and go to “Extensions > Utilities > Install Custom Dialog.”
- Select the downloaded PROCESS macro file and click “Open.”
- The macro will now be installed and accessible under “Analyze > Regression > PROCESS v3.5.”
- Verify Installation: After installation, restart SPSS and ensure that “PROCESS” appears in the Regression menu.
This setup will enable you to use the Hayes PROCESS Macro for advanced moderation and mediation analyses effortlessly.
Advantages of Hayes PROCESS Macro:
- Simplifies complex calculations.
- Generates comprehensive output, including interaction plots.
- Allows bootstrap confidence intervals for accuracy.
- Supports higher-order models and conditional process analysis.
3. Example for Moderation Analysis
Research Example: Imagine a scenario where a researcher is exploring whether the relationship between work hours and employee fatigue changes depending on physical activity levels. This example helps clarify the practical use of moderation analysis in real-world settings:
- Independent variable (X): Work hours
- Dependent variable (Y): Employee fatigue
- Moderator (M): Physical activity levels
4. Step-by-Step Conducting Moderation Analysis in SPSS
Using Regression Analysis
- Prepare the Data: Ensure all variables are entered and labelled correctly. Center the predictor and moderator variables to reduce multicollinearity.
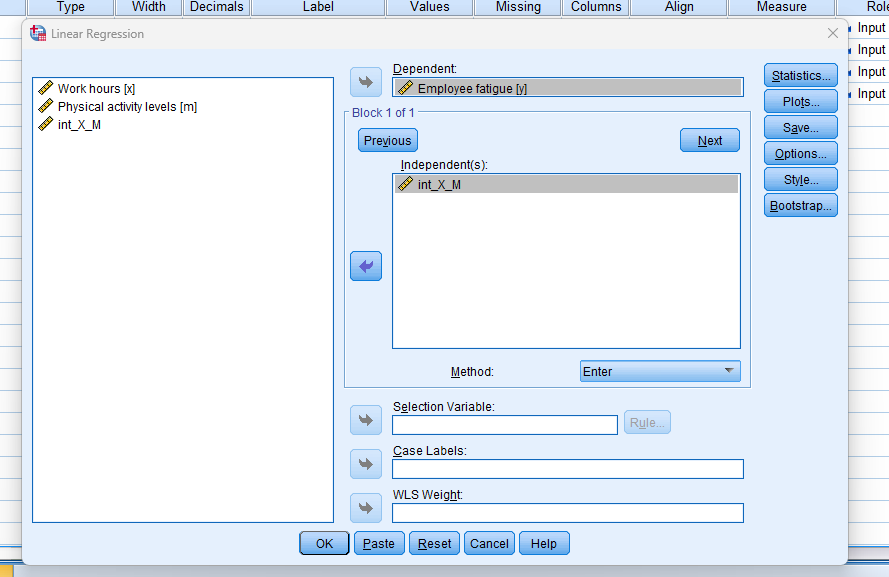
- Create Interaction Term: Multiply the predictor and moderator to create the interaction term (X*M).
- Run Regression:
- Open SPSS and go to “Analyze > Regression > Linear.”
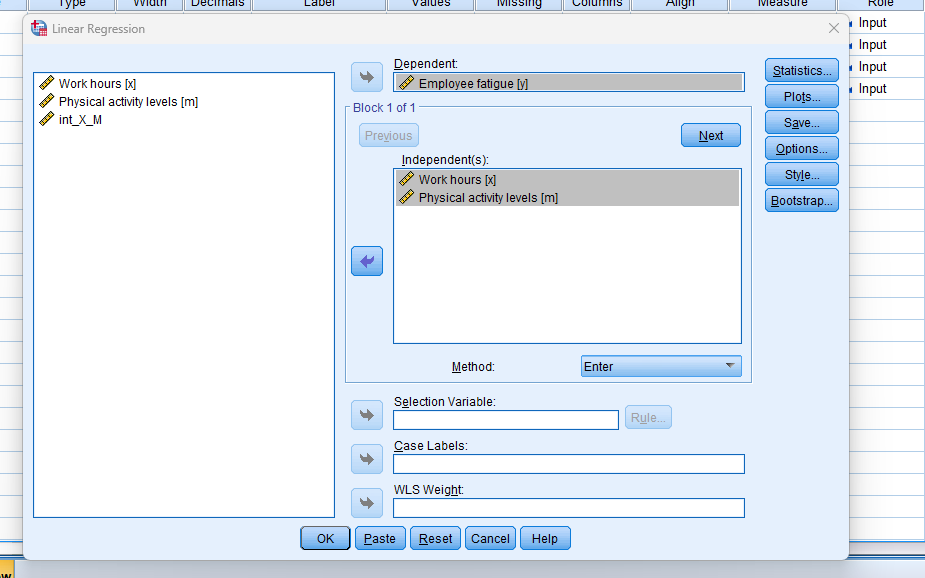
- Enter the dependent variable in the “Dependent” box.
- Add the predictor, moderator, and interaction term in the “Independent(s)” box.
- Interpret Results: Check the significance of the interaction term. If significant, moderation is present.
Hayes Process Macro
- Install the Macro: Download and install the PROCESS macro from Andrew F. Hayes’ website.
- Open the Macro: Navigate to “Analyze > Regression > PROCESS v3.5.”
- Input Variables:
- Define the dependent variable (Y), independent variable (X), and moderator (M).
- Configure Options:
- Select model 1 (moderation).
- Enable interaction plots and bootstrap confidence intervals.
- Run the Analysis: Review the output for the interaction effect and conditional effects.